あらすじ
幾何学を学んでいくと、位相という単語を聞き、その次に多様体という単語を聞くようになる。
私はゼニガメ→カメール→カメックスのように、
集合→位相空間→多様体と捉えている。
位相空間は集合に開集合を加えて考え、2つの位相空間の間に連続という関係を定めた。
では多様体は何を追加するか?
多様体では位相に座標近傍系を加えて考え、2つの多様体の間に微分という関係を定める。
微分とはなんだったか
微分とは、接線の傾きを求めるために編み出されたものだ。
そして直線は、2点を定めることによって一意に決まる。
そのことを用いて、2点を限りなく近づけるというアイデアで接線の傾きを求めることに成功した。
そのストーリーを感じながら、微分の定義をみてみる。
微分
関数\(f:\mathbb{R}\rightarrow \mathbb{R}\)について\(x=c\)で微分するとは、
\(\displaystyle{f'(c)= \lim_{h \to 0} \frac{f(c+h)-f(c)}{h} }\)を出すことである。
これはh分だけずらすと考えることができる。
さてこの少しずらすということは、位相でできるものなのだろうか。
これは、位相というものが集合に開集合という要素を加えたのみの世界であることを踏まえれば、
ずらすなんて全ての位相でできるとは限らないことがわかる。
そこで微分において重要な「ずらす」という操作を行うために
多様体では座標近傍系というものを導入する。
具体例とともにもう一度
例えば球面を考える.
球面であるx軸方向に少しずらすとどうなるだろうか?
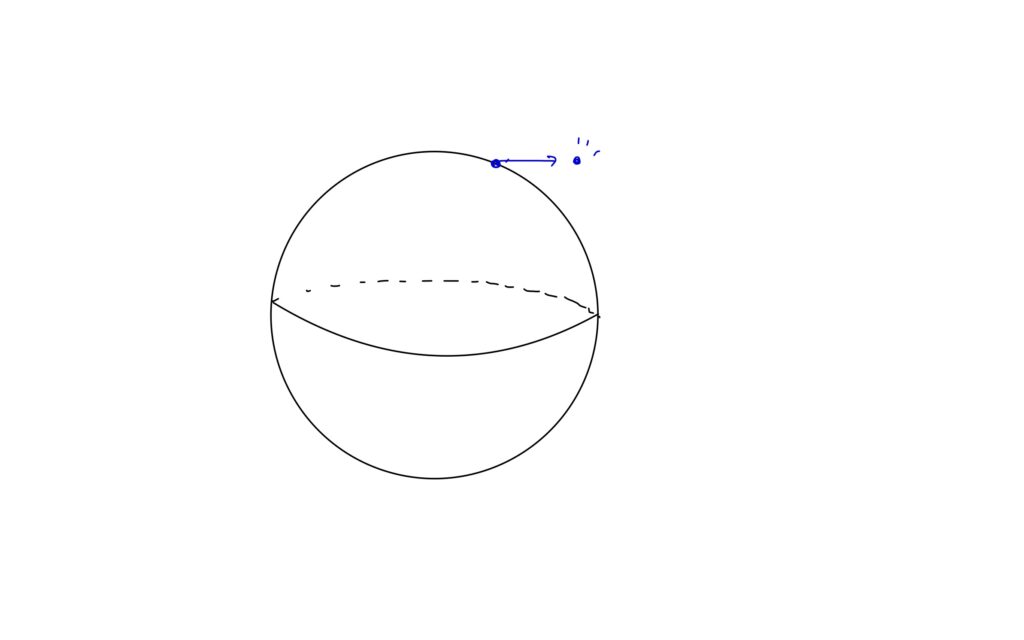
このように球面で「少しずらす」という操作を行うと、球面上から離れてしまい定義できない。
この不具合に対するアイデアとして、座標近傍系という道具を使う。
座標近傍系の気持ちを説明すると、「微分できる世界へ話を移し替える」ということだ。
このような気持ちを伝えたところでイントロダクションは終わりにする。
\(\)
コメント